TRIÁNGULOS
1. INTRODUCCIÓN
Con
origen en el latín triangulus, la palabra triángulo se utiliza
para identificar un polígono compuesto por 3 lados. Esta figura
geométrica se logra a partir de la unión de tres rectas que se interceptan en
tres puntos desalineados. Cada uno de estos puntos donde las rectas se unen
recibe el nombre de vértice, mientras que los segmentos que se pueden apreciar en la figura reciben el nombre de
lados.
2. DEFINICIÓN
Triángulo
es un polígono de tres LADOS, que viene determinado por tres puntos no
colineales llamados VÉRTICES.
1. ELEMENTOS DE UN TRIANGULO
Un triángulo tiene elementos primarios y elementos secundarios.
Los elementos primarios
corresponden a los vértices, lados y ángulos.
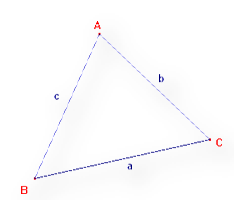
Los vértices son puntos de esquina de un polígono y se denotan
por letras mayúsculas: A, B y C;
Los lados son los segmentos que unen dos vértices del triángulo
y se denotan por la misma letra que el vértice opuesto, pero en minúscula. Es
decir:
El lado 'a', es el
segmento que une los vértices B y C.
El lado 'b', es el
segmento que une los vértices A y C.
El lado 'c', es el segmento
que une los vértices A y B.
Se llama ángulo de un triángulo, al
ángulo que forman las rectas sobre las que se apoyan
dos de sus lados incidentes en un vértice. El ángulo, se denota con la misma
letra que el vértice correspondiente.
1. CLASIFICACIÓN
DE TRIÁNGULOS
Los triángulos se pueden
clasificar según diferentes criterios:
a)
Por sus lados
b)
Por sus ángulos
a) Clasificación según sus lados
a.1 Triángulo
equilátero
Si sus tres lados tienen la
misma longitud (los tres ángulos internos miden 60 grados).
a.2 Triángulo
isósceles
Si tiene dos lados de la
misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.
a.3 Triángulo
escaleno
Si todos sus lados tienen
longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma
medida.
b) Clasificación
según sus ángulos
b.1 Triángulo
Rectángulo
Si tiene un ángulo interior
recto (90∘). A
los dos lados que conforman el ángulo recto se les denomina catetos y al otro
lado hipotenusa.
b.2 Triángulo
obtusángulo
Si uno de sus ángulos es obtuso
(mayor de 90∘); los
otros dos son agudos (menor de 90∘).
b.3 Triángulo
acutángulo
Cuando sus tres ángulos son
menores a 90°; el
triángulo equilátero es un caso particular de triángulo acutángulo.
BIBLIOGRAFÍA
Matemáticas,
Pedro Gutiérrez
Geometría y
Trigonometría, Aurelio Baldor







Muy buen trabajo para los estudiantes de secundaria
ResponderBorrarLa informacion es buenisima
ResponderBorrar